Ontwerpen van een 3D geprint riet
Het printen van rieten voor saxofoon en klarinet wordt door sommigen al gedaan en is vooral voor de dure grote rieten erg interessant. Het voordeel van een geprint riet is dat je op den duur ook af kunt wijken van de vorm die voor een groot deel bepaald is door het oorspronkelijke materiaal; de bamboo stengel. Maar laten we eerst maar eens met een basis riet beginnen. Hoe zit die eigenlijk in elkaar?
De belangrijkste maten van een riet zijn de afmetingen, de lengte en de breedte aan de voet en de tip en de dikte. Voor de grootste rieten heb ik de volgende maten gemeten:
| Breedte voet | breedte tip | lengte | ronding tip | lengte snede | dikte | |
| sopraansax | 12 | 14 | 60 | 2.5 | 3.5 | |
| altsax | 13 | 17 | 70 | 4 | 3.1 | |
| tenorsax | 15 | 17 | 81 | 3.5 | 3.9 | |
| baritonsax | 16*-17,5 | 18.4*-19.5 | 91* | 3.5* | 49.5* | 3.2* |
| bassax | 17* | 21* | 98* | 3.7* | 52.5* | 4.5* |
| Bb klarinet | 11.5 | 13 | 68 | 2.5 | ||
| basklarinet | 14.5* | 17* | 78* | 3.1* | 40* | 3.7* |
| contraaltklarinet | 16.3* | 18.9* | 90* | 3.7* | 48* | 3.7* |
| contrabasklarinet | 17.2* - 18 | 19.5* | 86.5* | 3.7 | 48* | 3.9* |
* is gemeten waarde, overige waarden van internet
Het ontwerp maak ik in OpenScad.
De basisvorm
De data is verzameld in een array
|
reed = w_btm = reed[type][1]; |
Van de lengte en breedte maten wordt de rechthoekige vorm van het riet gemaakt.
| module basic_shape() { translate([0,0,0]) linear_extrude(2*d_btm_mx) polygon(points=[[0,0.5*w_btm],[length-tip_curve,0.5*w_tip],[length-tip_curve,-0.5*w_tip],[0,-0.5*w_btm]]); } |
en dat levert de volgende vierhoek op:
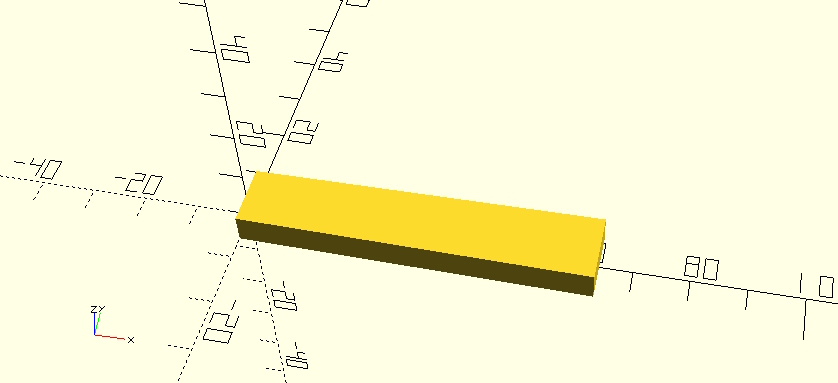
De tip van een riet is een ellips. De ene straal is gelijk aan de halve breedte van de tip en de ander is opgemeten en bedraagt iets tussen de 3 en 4 mm. De ellips is eenvoudig te maken door middel van een resize van een cirkel:
| module tip_ellips() { translate([length-tip_curve,0,0]) resize([tip_curve*2,w_tip,2*d_btm_mx]) cylinder(h=2*d_btm_mx,d=w_tip); } |
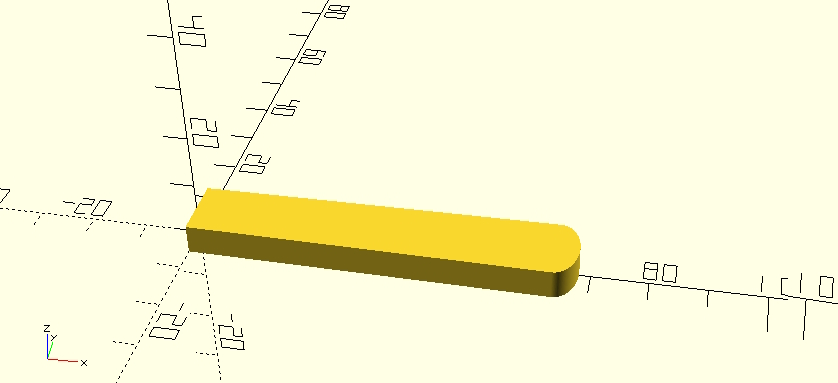
De vorm wordt vervolgens net als een echt riet afgerond. De basis voor de afronding vormt de opgemeten maximum dikte. In de praktijk blijkt dat de rieten onderling erg verschillen. De functie is ook niet heel belangrijk. Het moet goed passen onder de rietbinder en die gaat meestal uit van een ronde vorm.
| module top_curve() { S = w_btm/2; d =d_btm_mx-d_btm_mn; cane_diameter = 2*S /sin(2* atan(d/S)); translate([0,0,-cane_diameter/2+d_btm_mx]) rotate([0,90,0]) cylinder(length, d=cane_diameter); } |
De vorm wordt gerealiseerd door een intersection met een cylinder met de diameter: cane_diameter. Er onstaat al een rietachtige vorm:
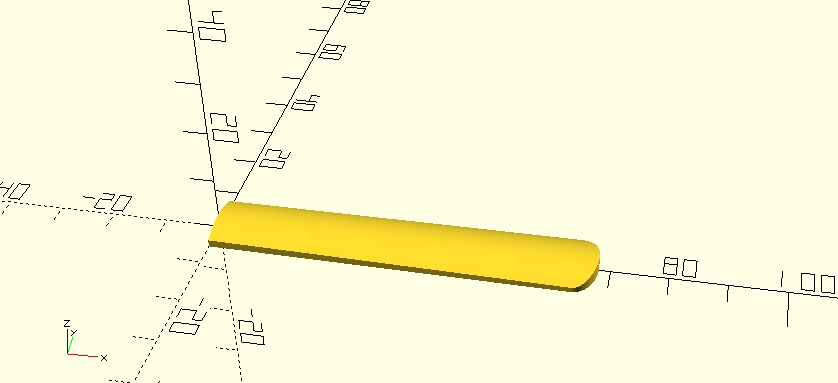
Nu volgt het belangrijkste stuk; de uitsnede van het riet. Er is weinig informatie te vinden over deze curve maar als je een riet goed bekijkt blijkt het een complexe vorm te zijn. Allereerst is er de ZX curve. Dit is vermoedelijk een soort van boogvorm die ongeveer 50% van de lengte van het riet wegsnijdt en eindigt bij de tip. Maar in de Y richting varieert de curve ook. In het midden is het uitsnede hoger dan aan de zijden. Er zijn zelfs bijzondere manieren van snijden zoals de american cut van Legere:

Dit is wel interessant want het illustreert de vele mogelijkheden die er zijn als je rieten in 3D ontwerpt en print.
Bij nameten blijkt de aanname dat de snede volgens een cirkelsegment verloopt goed te kloppen voor de zijkanten van het riet. In het midden lijkt het riet haast in een rechte lijn gesneden.
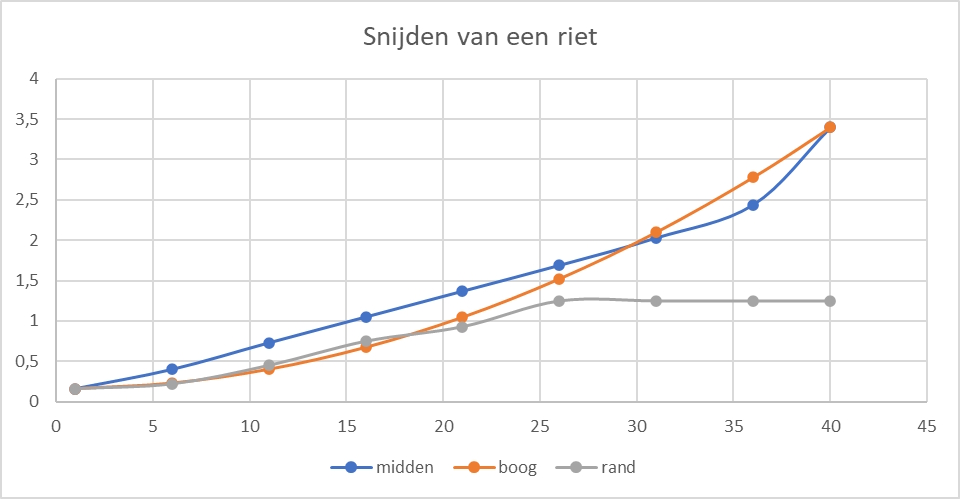
Het blijkt dat de middencurve vrijwel gelijk is aan het gemiddelde van de rechte lijn en de cirkelvorm van de zijkanten. Deze curve is geimplementeerd in de eerste versie van het programma. Mogelijk volgen nog meer versies als de inzichten wijzigen. Het bestand is hieronder te downloaden.

Benaming van de onderdelen van het riet
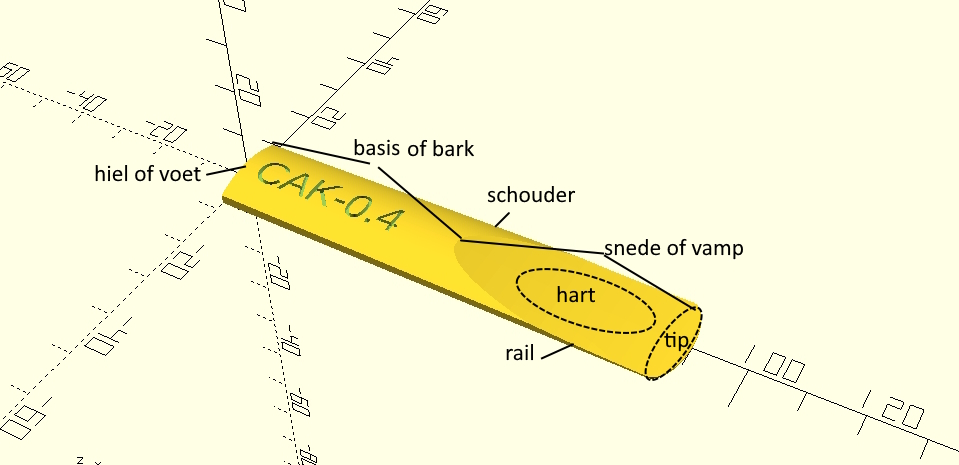
De snede of vamp is het deel van het riet wat trilt en de opening (window) van het mondstuk afsluit.
De tip is verantwoordelijk voor de hoogfrequente bewegingen van het riet.
Het hart van het riet is wat dikker dan de zijkanten, de rails.
De basis of bar is het deel waarmee het riet op het mondstuk wordt geklemd.
De schouder is de overgang van de basis naar de snede. Bij sommige rieten wordt de schouder rond gevijld. Dit wordt french cut genoemd. Er wordt beweerd dat dit de hoge boventonen in de klank van het instrument ten goede komt.

Het verschil tussen een saxofoon en een basklarinet riet
Op de website van vandoren is wel informatie te vinden over de verschillen tussen de verschillende type rieten (zie : https://vandoren.fr/en/reeds-technical-elements/). Er zijn vier verschillende klarinet rieten en zeven verschillende saxofoon rieten.
De verschillen worden weergegeven door middel van hoogtelijnen. Daardoor wordt zichtbaar dat met name het hart van het riet anders ontworpen is. De dwarsdoorsnede van het hart varieert van een netto boog tot een afgeplatte boog. Bij de saxofoonrieten zijn de dwarsdoorsnede vooral aan de voorzijde meer afgeplat. Ook is het verschil in dikte tussen het hart en de rails bij een saxofoonriet groter.
De conclusie is in ieder geval dat het ontwerp van het 3D riet moet worden aangepast.
Aanpassingen versie 2p0
De eerste aanpassing die is gemaakt is de basisvorm van de snede.
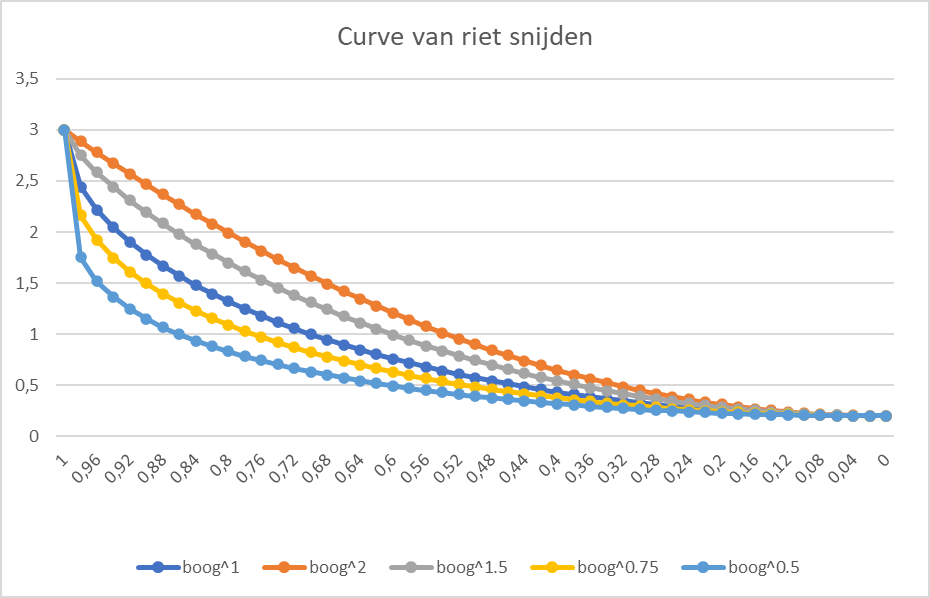
De basisvorm van de snede is bepalend voor de zijkanten van het riet; de rails. Uitgangspunt is in eerste instantie een boogvorm. De straal van de boog is gelijk aan de lengte van de snede. In de hoogte richting is die afgeplat tot de diepte van de snede (die is circa 2mm). Die vorm blijkt niet helemaal stijl genoeg. Dit is op te lossen met een powerfactor. Door de boog te beschouwen als een sin/cos curve en de verticale component tot een macht te verheffen blijft de otale hoogte gelijk. In de grafiek is de middelste donkerblauwe curve de afgeplatte boog. De curve daaronder een macht van 0,5 of 0,75 en daarbvoen van 1.5 en 2 van de verticale component.
De middellijn dwars door het hart van het riet is bij sommige rieten een rechte lijn.
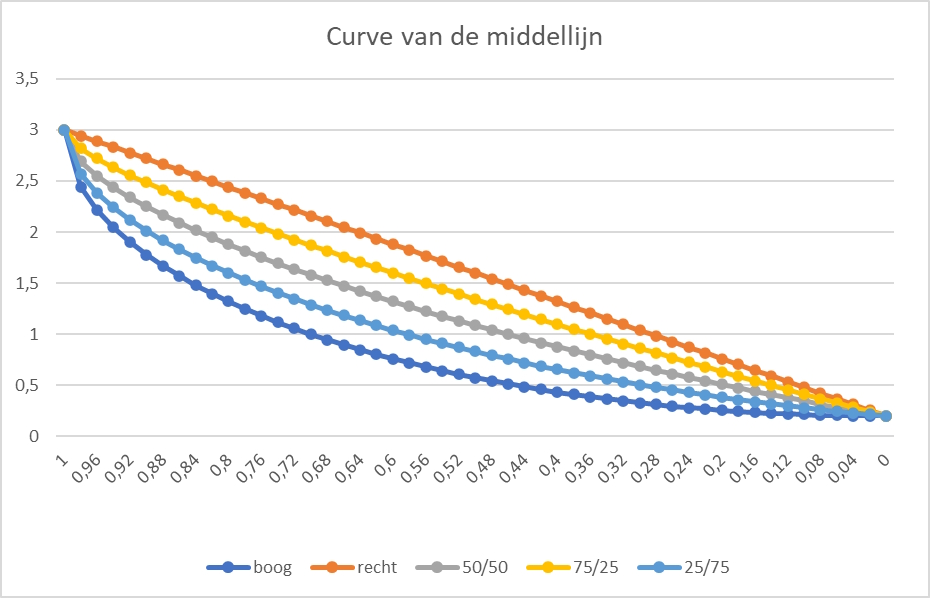
Maar meestal is de curve het gemiddelde van een rechte lijn curve en de boogcurve van de zijkant van het riet. De grafiek hierboven toont de lijnen voor verschillende verhoudingen van de twee curves.
Het midden van het riet ligt altijd hoger dan de zijkant. De curve door de top en de zijkanten is ook weer een afgeplatte cirkel of een machtsfactor daarvan.
In totaal zijn er voor de vorm van de snede dus de volgende parameters:
-
- powerx - de machtsfactor voor de curve in de x richting (varierend van 0.5 tot 2) van de tip naar ongeveer halverwege de lengte van het riet.
- powery - de machtsfactor voor de curve in de y richting van het hart van de snede naar de zijkant
- m_factor - verhouding tussen de rechte lijn curve en de gebogen curve voor het hart van het riet.
Hieronder zijn een aantal voorbeelden van de hoogtelijnen die ontstaan als functie van de parameters:
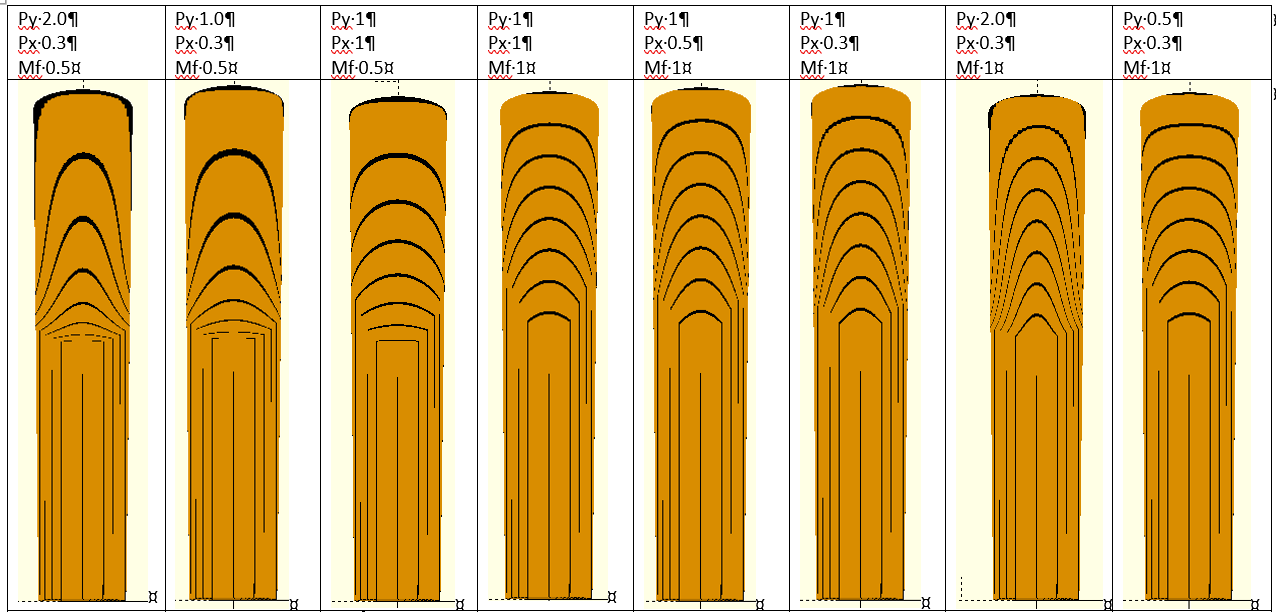
Voorlopige favoriete waarden
- Een beste waarde voor powerx is 0.5
- Powery = 1 en m_factor 1 benaderen goed het traditional klarinet reed van Vandoren
- Powery = 1 en m_factor 0.5 benaderen goed het V12 riet voor klarinet
- Powery = 0.5 en m_factor 1 benaderen goed het traditional saxofoon riet
- Powery = 0.5 en m_factor -1 en Powerx = 0.3 voor een Java saxofoon riet
Software
20230923 versie met gebruik van sweep functie, introductie van powerx en powery om snede te configureren. basensax reed v2p0.scad
20230917 initiele versie eigen ontwerp: basensax reed v1p0.scad
Links
[1] Contrabas: https://www.thingiverse.com/thing:5206429
[2] Bariton: https://www.thingiverse.com/thing:2873379

-1666348987.jpg) We zijn het adres voor het huren van basklarinetten en saxofoons.
We zijn het adres voor het huren van basklarinetten en saxofoons.



